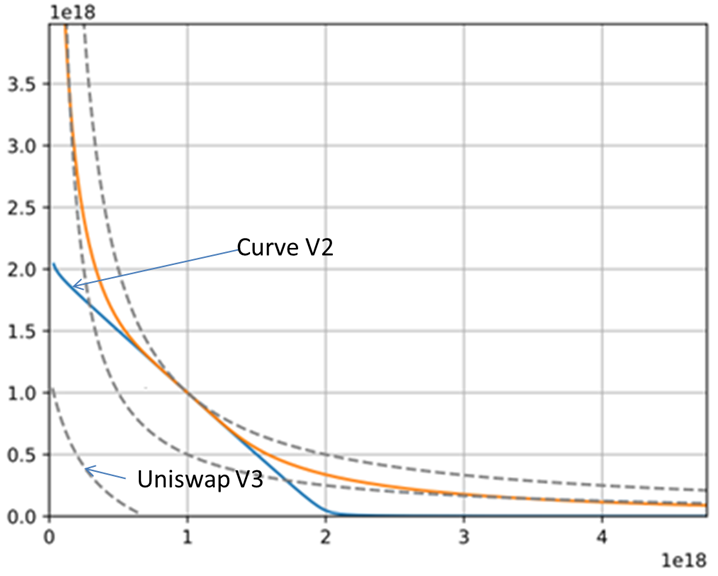
上一篇文章我们通过数据比较了curve和uniswap V3的滑点差异,可以发现,在可比条件下,uniswap V3的滑点小于curve,那么这是为什么呢?今天我们就从两者的技术原理出发,分析一下为什么curve的滑点会大于uniswap V3。Curve采用的恒定乘积和恒定和的混合曲线方程,,我们知道在恒定和的做市曲线下,兑换是没有滑点的,但流动性是有限的,而恒定乘积做市曲线下,兑换是存在滑点的,但流动性是无限的,curve将以上两者曲线结合起来,提出了一种混合做市曲线:
A(P0x+y)+xy=k
P0为平衡点价格
对上式求导可以得到价格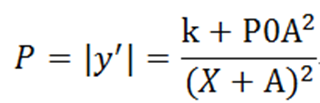
当A趋近于无穷大时
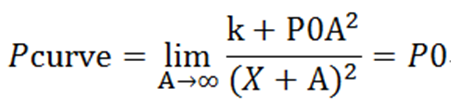
因此A越大,兑换价格越接近于P0,即滑点越小,
而根据uniswap V3的做市曲线,
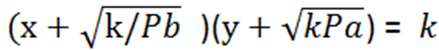
同样可以得到兑换价格
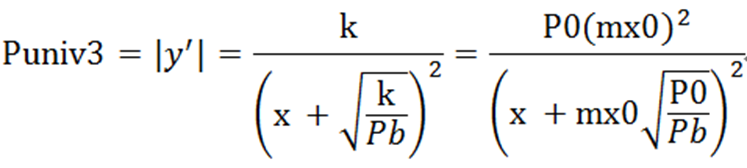
m为x的放大系数
当m趋近于无穷大时
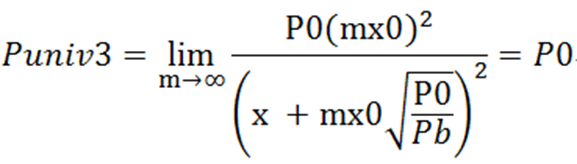
从上面可以看出curve的兑换价格与A强相关,而uniswap V3的兑换价格与m强相关,而我们知道curve中放大系数A是由协议内部决定的,外部用户无法改变,而uniswap V3的放大系数m完全由外部流动性提供者设定的价格范围决定的,如将m值等效于curve中的A,即理论上uniswap V3可以放大无限倍,而curve为了保证无限的流动性,放大系数A不可能无限大,因此curve的滑点必然会大于uniswap V3。